主成分分析をエクセルの中でClaudeを使って実施 〜Claude in excel

財務諸表の分析などを実施したので、次は統計処理的なことをClaude In Excelでやってみます。
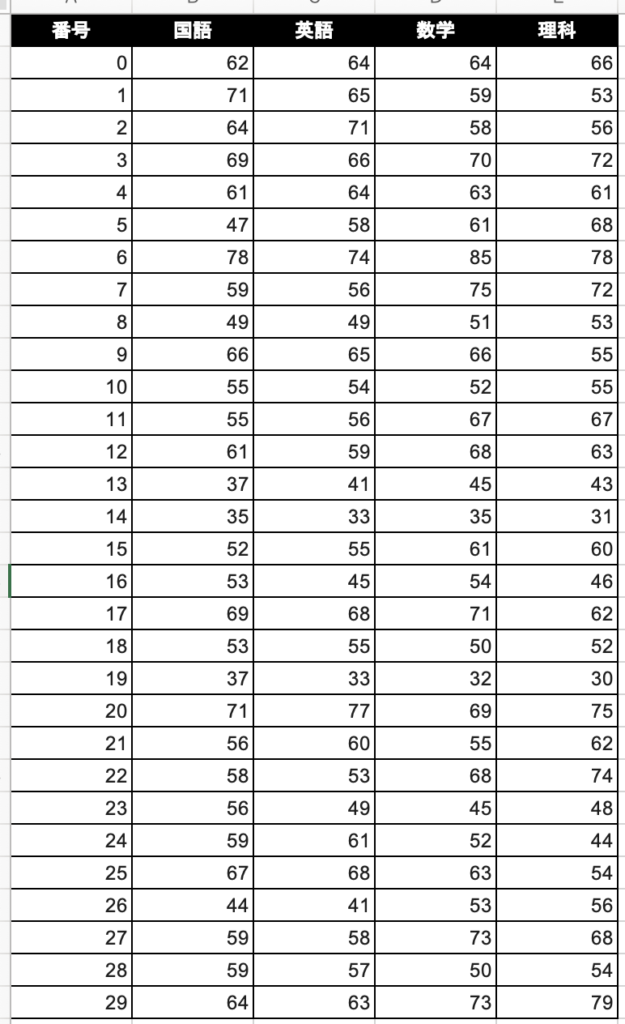
サンプルデータ
4科目の点数のデータを作りました。 理系とか文系、総合格力の視点で分析してくれるかな。
Claude in Excel2お願いする
もう、そのままンマ、お願いしました。「主成分分析をしてください」

出力結果
Claudeの実行プロセス

分析結果
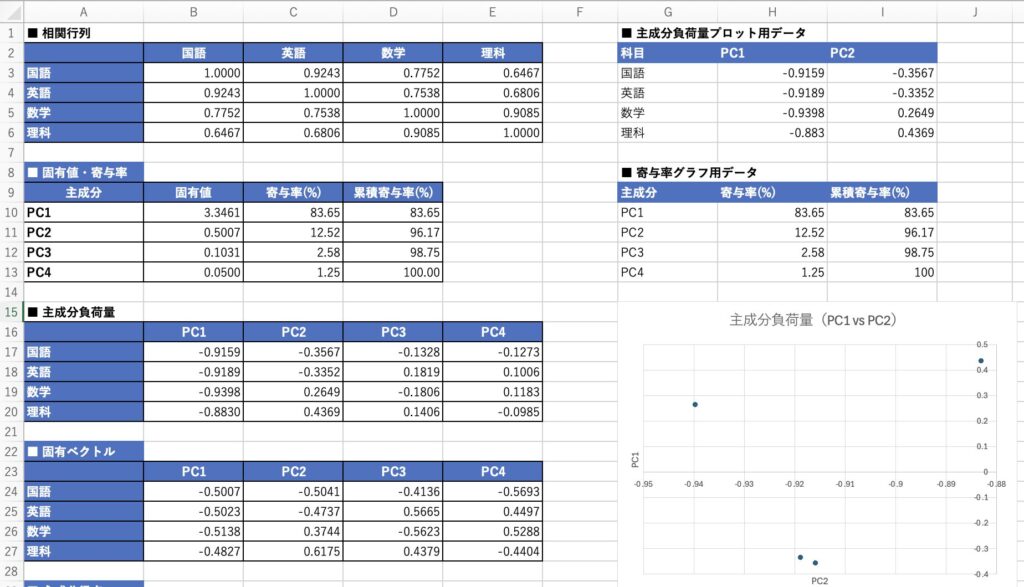
1. 相関行列
- 国語と英語の相関が最も高く(0.924)、文系科目同士の強い関連
- 数学と理科も高い相関(0.909)、理系科目同士の強い関連
2. 固有値・寄与率
| 主成分 | 固有値 | 寄与率 | 累積寄与率 |
|---|---|---|---|
| PC1 | 3.35 | 83.65% | 83.65% |
| PC2 | 0.50 | 12.52% | 96.17% |
| PC3 | 0.10 | 2.58% | 98.75% |
| PC4 | 0.05 | 1.25% | 100.00% |
→ PC1とPC2の2成分で全体の96.17%を説明できます。
3. 主成分の解釈
- PC1(総合学力): 全4科目の負荷量がほぼ均等に高い(-0.88〜-0.94)。すべての科目に共通する「総合的な学力」を表します。
- PC2(文系 vs 理系): 国語・英語がマイナス方向、数学・理科がプラス方向。文系タイプか理系タイプかの違いを表します。
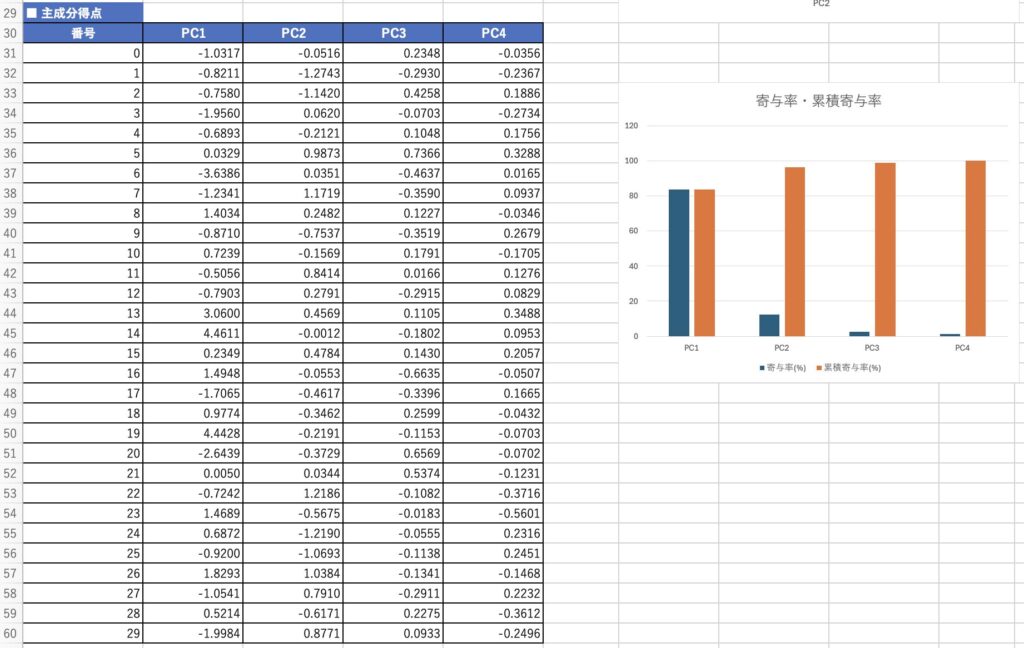
4. チャート
- 主成分負荷量の散布図(PC1 vs PC2)
- 寄与率の棒グラフ(個別寄与率 + 累積寄与率)
数式
一言で、ザーッとここまでやってくれるのは嬉しいですね。今回は数式はのこしてくれなかったので、数式を残してよとお願いしました。(無理だろうなとおもいつつ)
でもやれるところだけはやってくれるみたいです。

相関行列の関数は入りましたね。
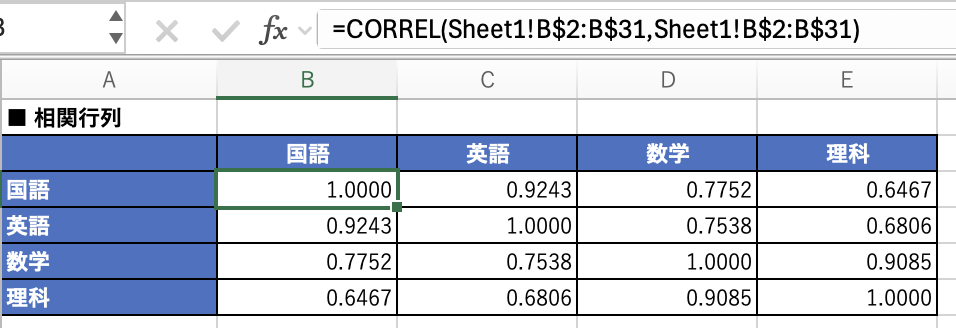
途中の固有値やベクトルなどは数値になっていましたが、主成分得点にはなにか数式が入っていますね。
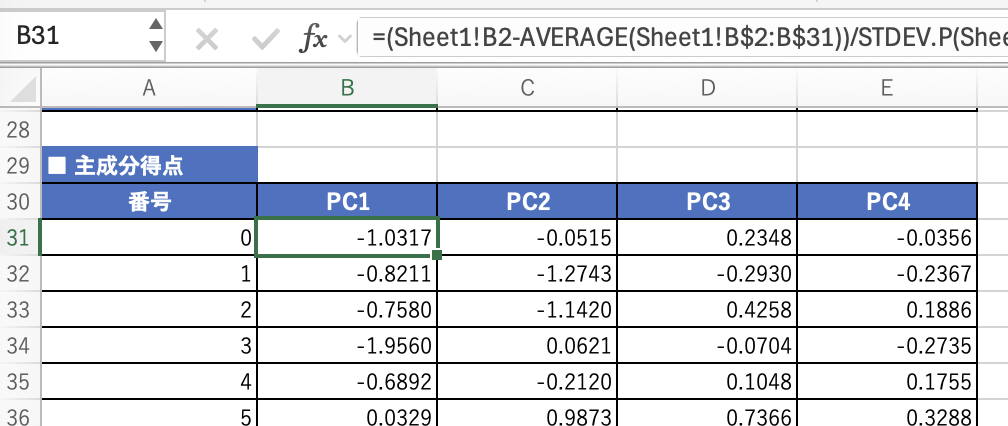
ということで、なにか計算してくれていました(^^^;
=(Sheet1!B3-AVERAGE(Sheet1!B$2:B$31))/STDEV.P(Sheet1!B$2:B$31)$B$24+(Sheet1!C3-AVERAGE(Sheet1!C$2:C$31))/STDEV.P(Sheet1!C$2:C$31)$B$25+(Sheet1!D3-AVERAGE(Sheet1!D$2:D$31))/STDEV.P(Sheet1!D$2:D$31)$B$26+(Sheet1!E3-AVERAGE(Sheet1!E$2:E$31))/STDEV.P(Sheet1!E$2:E$31)$B$27
感想
まあこういった理系・文系分析は、例題としてよく見かけますが、実際のところはどうなんでしょうね。
数学の点数トルには出題の意図を把握しないといけないので、国語力が必要とよく言われますが。
そんなところで

