普通と呼ばれる男性は0.8%しかいないのか?

なぜ“普通のオトコ”は、なかなか見つからないのか?
http://bizmakoto.jp/makoto/articles/1204/26/news005.html
普通の会話50%
×普通のルックス50%
×普通の身長50%
×普通の清潔感50%
×普通のファッションセンス50%
×普通の学歴50%
×普通の年収50%
=0.8%
上記をすべて満たす
普通の男性は 0.8%しかいないらしい。
つまり、普通の男性は 0.8%しかいない。 そんな、あほな。
そもそも、
普通という要素を 5割と規定したことがこの場合はおかしい。
さらに、これらの項目は多分に相関関係がありそうなので、
単純に掛けあわせればいいのかも疑問が残る。
この場合の普通は、9割くらいが普通なのかもしれない(^^;
0.9 を 7回かけると 約48%
なんとなく、普通っぽい。
さて、中小企業診断士の2次試験合格への確率はどんなもんだろうか?
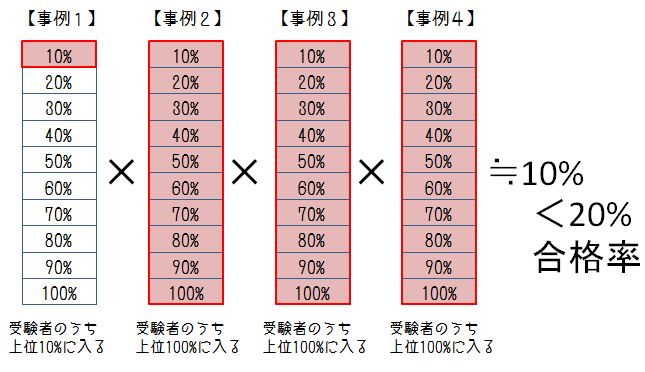
合格率は、年度によりばらつきも大きいが、概ね、20%弱。
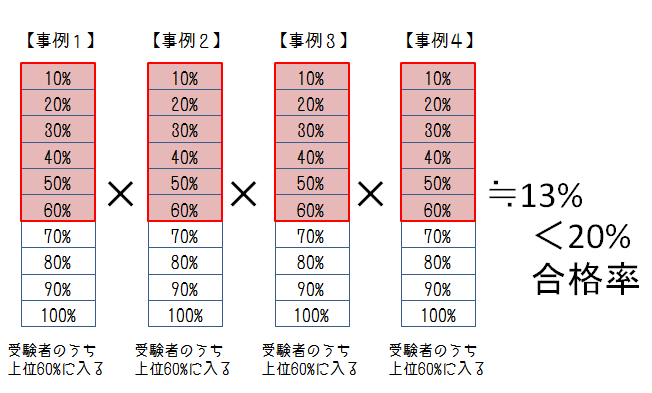
4科目合計で上位2割に入るには、各科目の上位6割に入ればいいということになる。
※実際に、昔、予備校の模試で点数データを分析した際は、
各科目で上位4割には行っている人は、十分合格点であった。
しかし、この計算が成り立つとすると、以下のパターンでも合格できるのかもしれない。
(足切りは除く: 実際問題、本試験でDの足切りが付いている答案はかなり少ない。
これも、H18に初めてランクがついたときに、ふぞろいで分析したときは
D答案の割合は1%程度であった。近年増加傾向にあるが、それでも
Dの数は圧倒的に少ない、と思われる)
上記2つのモデルの欠点は、診断士試験の得点分布を無視していることだ。
実際の得点分布データがないので、なんとも言えない。
でも、正規分布していると考えると、十分成り立つと思う。
(60点前後と 50点前後の二山ある分布か、
イレギュラーな分布図になっている可能性もあるが)
まあ、
・各科目バランスよく4割くらいの位置をキープ出来れば合格できるし、
・1科目だけ上位数%に入っても逆転できる というのが 一応の結論か。。
(財務で一発逆転の人がいる事象が説明できる)
いずれにせよ、こんな確率論を考えているのは時間の無駄である。
そんな感じで。